Introduction to Category Theory

In our previous articles, we discussed the significance of functional composition in functional programming, and provided an example of how it can result in code that is easier to test and maintain. However, what happens when two functions cannot be composed? How can we overcome this issue? Fortunately, many researchers and mathematicians have dedicated themselves to developing a theory focused on composability: Category Theory.

Category Theory is a branch of mathematics that provides a way to study and understand the structures and relationships between different mathematical objects in a very general and abstract way. It does this by looking at the patterns and connections between these objects and their transformations.

Category Theory was founded by Saunders Mac Lane and Samuel Eilenberg in 1945.

Definition

A category is a pair (tuple) of (Objects, Morphisms) where:

• Objects is a collection of objects
• Morphisms is a collection of morphisms (also called “arrows”) between objects

Please note that the term object has nothing to do with the objects in the context of software engineering and programming. You can think these Objects as black boxes that we can’t know what’s inside.

For every Morphism there is a source Object A and a target Object B. We write f: A ⟼ B and we say that “f is a morphism from A to B”.

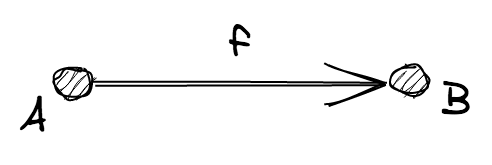
There is also, an operation, ∘, called “composition”, such as the following properties hold true:

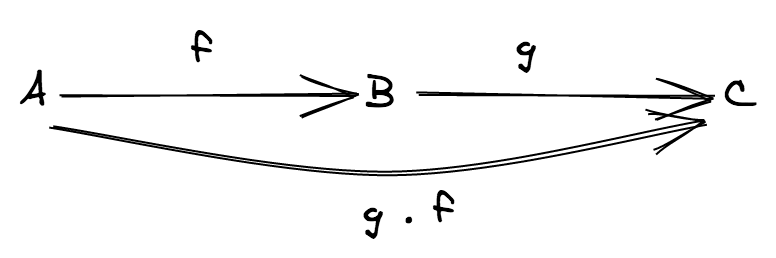
• Composition of morphisms: Given the following morphisms f: A ⟼ B and g: B ⟼ C then there has to be a third morphism g ∘ f: A ⟼ C which is the composition of f and g

• Associativity: if f: A ⟼ B, g: B ⟼ C and h: C ⟼ D then h ∘ (g ∘ f) = (h ∘ g) ∘ f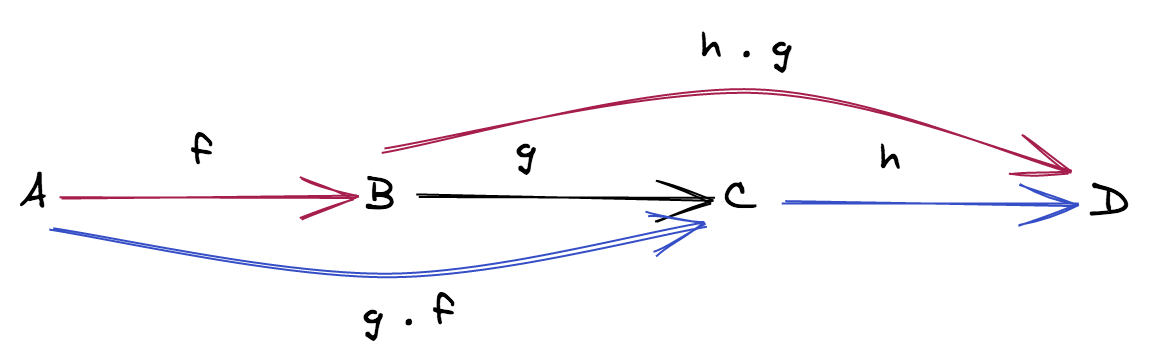

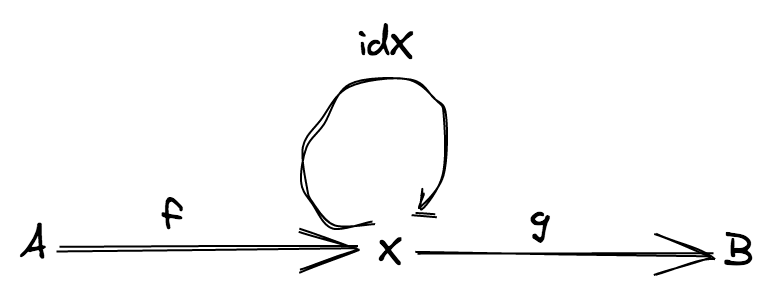
• Identity: for every object X, there is a morphism called identity: X ⟼ X such as for every morphism f: A ⟼ X and g: X ⟼ B, the following equation holds true identity ∘ f = f and g ∘ identity = g.

Category Theory in Software Engineering: Modeling programming languages with categories.

A category can be seen as a simplified model for a typed programming language, where:

• Objects are types.
• Morphisms are functions.
• ∘ is the usual function composition.

Lets consider the following Category:

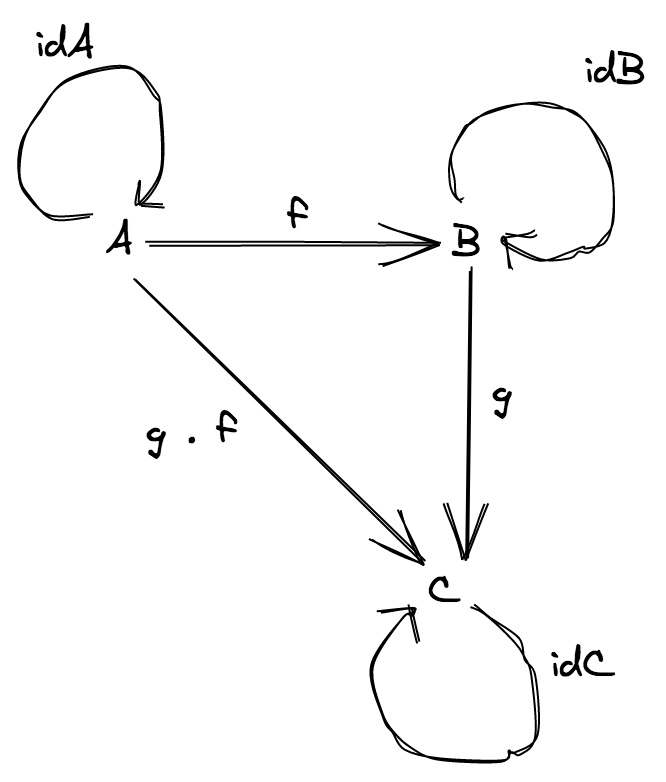
Given that:

• A = string
• B = number
• C = boolean
• f = string => number
• g = number => boolean
• g ∘ f = string => boolean

The implementation of this category in typescript would be the following:

const idA = (value: string): string => value;
const idB = (value: number): number => value;
const idC = (value: boolean): boolean => value;

const f = (s: string): number => s.length;
const g = (n: number): boolean => n > 0;
const gf = (s: string): boolean => g(f(s));

Composition’s core problem

In programming, we can compose two generic functions, f: (a: A) => B and g: (c: C) => D, as long as C is equal to B. However, what if B is not equal to C? How can we compose two functions in such a scenario? Is giving up the only option?

In the next article we’ll see under which conditions such a composition is possible. We will also explain the concept of a Functor, an Applicative Functor and a Monad.

Resources:

• Enrico Polanski - functional programming